The
speed of Light
MOTIVATION:
One of the questions that bothered early scientists concerned the speed of light. From simple observation, it is obvious that light travels much more rapidly than sound. But how fast does it travel? And how can you measure something that travels so fast?
The first experiments to measure the speed of light seem to have been done by Galileo, using shuttered lanterns atop two mountains several kilometers apart. However, human reaction time to open and close a shutter swamped the actual time of transit for the light, and Galileo reported that the speed must be near infinity.
The first non-infinite value of the speed of light was reported by Olaus Roemer, a Dutch astronomer, in 1675. He reported a speed of light based on small discrepancies in eclipse times for Jupiter's moons, which he correctly analyzed to vary because of the changing distance between the earth and Jupiter as they orbited the sun.
It was not until the experiments of the French scientists, Fizeau and Foucault, in 1849, that a value close to the currently accepted speed of light was reported. Their experiments were within 5% of the correct speed of light. Their methods were improved by several, but especially Albert Michelson, whose experiments between 1878 and 1926 on the speed of light were marked by great precision.
SPECIFIC OBJECTIVES:
When the student has completed the experimental activity, he will: (1) have measured the time delay of a light signal passing through an optical fiber as a function of fiber length; (2) have computed the speed of light passing through the fiber; (3) have computed the index of refraction and the dielectric constant of the fiber; and (4) have computed the absorption coefficient of the fiber.
THEORY:
Optical Fibers:
When a ray of light passes from a transparent material such as glass or water into the air, the ray is refracted, or bent, away from the normal of the interface surface. Snell's Law, which governs such refraction, provides an upper limit for the incident angle at which refraction can take place. The basic statement of Snell's Law is:
![]() (1)
(1)
The upper limit is found by letting q 2 go to 90°, for which the sine has its maximum value of 1.000. Then,
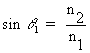 (2)
(2)
and when using air for the refracting medium (n2 = 1.00), then
![]() (3)
(3)
Since the index of a transparent material must be greater than 1.00, the ratio determines a maximum angle, q , for refraction to occur. If light is incident at an angle larger than this maximum, no refraction occurs and the incident light is totally reflected at the surface. This is referred to as total internal reflection (TIR), and is a phenomenon that is widely employed in optical devices where light must be reflected.
Total internal reflection is also used to conduct light down a narrow channel, such as a tiny glass fiber, for purposes of communication and remote viewing. The advent of small, intense sources such as diode lasers, coupled with improvements in the purity of glass to reduce the absorption of light over large distances, has propelled optical fiber telephone circuits from a laboratory curiosity to a commercial reality. The medical profession has likewise benefited from the creation of endoscopes, which permit the viewing of interior regions of the body without major surgery.
Speed of Light in a Fiber:
The speed of light as it travels through a transparent material is somewhat slower than the speed of light in a vacuum, which we know to be 2.9979 x 108 m/s. Because light is an electromagnetic wave, its velocity will depend on the dielectric constant and the magnetic constant for the material it is traveling through. For most materials, the magnetic constant can be taken to be 1.0, which means that the dielectric constant of the material determines the speed at which light travels.
In optics, the ratio of the speed of light in a vacuum to the speed of light in a transparent medium or material is called the index of refraction, or:
![]() (4)
(4)
where n always has a value greater than or equal to 1. The index of refraction is crucial to the formulation of Snell's law and many other aspects of optics. In many instances, it is easier to measure the index of refraction to determine the velocity of light in a material. For this experiment, however, you will measure the actual velocity of light in the material, and determine the index from its definition in equation (4).
Once the index of refraction is known, the dielectric constant of the material can be found by using the relation that:
![]() (5)
(5)
This value of the dielectric constant may not be the same as found in tables in your textbook, for it is the dielectric constant at optical frequencies on the order of 1014 Hz rather than the much lower frequencies of typical electrical circuits.
Absorption Coefficient:
As light travels through a transparent medium such as glass, it occasionally encounters impurities which tend to scatter some of the light randomly. The scattered light is no longer available as part of the signal, and thus the signal intensity is reduced. In this experiment, as longer lengths of cable are used, the intensity of the received signal will be reduced, and the amplitude of the signal displayed on the CH2 trace will be smaller.
The fraction dI/I of the intensity lost in traversing an infinitesimal thickness dx is proportional to dx, so that:
![]() (6)
(6)
where the proportionality constant, a , has units of reciprocal length and is called the absorption coefficient. The sign is negative because the intensity is reduced as the thickness is increased.
At your station, you should find a dual trace oscilloscope, a circuit board, and several coiled lengths of optical fiber cable. Separate the cables by length, and carefully measure and record the cable lengths. The cables will be used, one at a time, by inserting the cable ends into the cable connectors on the circuit board. The cable is removed by loosening the clamp and gently pulling the cable straight out from the connector. Do not bend the cable as you pull. Remove any optical cable that may be connected to your circuit board at the present time.
In order to measure the very short times associated with transmittance through the optical fiber, we will use a dual trace oscilloscope and measure the time displacement of the received signal relative to the transmitted signal. Attach the 'scope lead from CH1 to the BNC connector on the circuit box marked "CH1" and the 'scope lead from CH2 to the BNC connector marked "CH2." Plug the power cord into the BNC connector on the circuit board.
Turn on the oscilloscope, and set the Time/Div control to .5 or .2 µs/cm. Set the VOLT/DIV switches for both CH1 and CH2 to 1 Volt. Be sure the variable on all three of these controls is in the CAL position. If you need to review the control functions of the oscilloscope from the previous experiment, be sure to do so. These values are initial settings only, and should be adjusted as necessary by the experimenter to optimize the measurement of the data.
Plug in the power transformer for the circuit. You should be able to see the LED at the "CH1" cable connector glowing red if you look in at it. If it is not glowing, you have a problem, and should seek help from the instructor immediately. You should also see a signal on the CH1 trace of the 'scope, but the CH2 trace will be flat until the optical cable is connected.
Now connect the shortest optical fiber cable between the cable connectors on the circuit box. The CH2 trace should now show a signal, which is similar in shape to the CH1 trace, but displaced slightly to the right of the CH1 trace. The task is now to measure as carefully and accurately as possible the amount of displacement between the two traces. Adjust the 'scope settings as necessary to measure the time delay between the two signals. Record the fiber length and the amount of time delay, using appropriate units for each measurement. Also, measure the amplitude of the received signal (CH2), and record it in a column of your data table.
Now remove the optical cable, and replace it with the next longer one. The displacement should be slightly larger than before. Again, measure the time displacement between the two signals and record in your data table. Measure and record the amplitude of the received signal as before. Continue the procedure with each optical fiber until all have been measured.
ANALYSIS:
Speed of Light in the Fiber:
To determine the speed of light in the optical fiber, plot the time delay data as time delay versus fiber length. Be careful about the units, and especially the numeric value of unit prefixes. The data should plot as a reasonably straight line, which has a slope equal to the reciprocal of the velocity. Use a linear regression, either on your calculator or with Excel, to determine the best value of the slope. Record your value of velocity, and also compute the value of the index of refraction, using equation (4), and the value of the dielectric constant, using equation (5).
You should probably note that the electronics of the circuit box introduces a noticeable time delay in the signal. By using the linear fit, that delay is treated as a constant for all data points, and does not affect the value of the slope.
ABSORPTION COEFFICIENT:
The absorption coefficient can be found from the data relating the signal amplitude to the fiber length. However, since the function is an exponential, we should plot log I versus fiber length, rather than just I versus length. The graph of log I vs. length should be a descending straight line, with slope equal to -a . Again, use a linear regression to determine the best value of the slope. Record the value of the absorption coefficient, including its units.
FINAL SUMMARY:
Your final summary should include the values for the speed of light in the fiber, the index of refraction of the fiber, the dielectric constant of the fiber, and the absorption coefficient of the fiber. In addition, you should consider the following items, and answer based on what you have observed in this experiment:
- How long will it take light to travel 1 foot in the
fiber? 1 meter? 10 meters?
- Why can you not compute the index of refraction for
glass by referring to the table of dielectric constants in your textbook?
- What is the maximum length of fiber that light can
traverse if its intensity is to be at least 50% of the original intensity?
What distance if the intensity can be as little as 10% of the original?