![]() (1)
(1)
THE LATENT HEAT OF VAPORIZATION OF NITROGEN
View cup with liquid nitrogen on scale
View mass being placed in a cup of liquid nitrogen
View mass being transferred to calorimeter
RATIONALE:
Physics is concerned not only with discovering the basic laws that govern the behavior of matter and energy; it also seeks to determine the properties of materials to which these laws are applied. These properties may include the mass and electric charge of elementary particles. They also include elastic, thermal, optical, and electrical properties of matter. In this experiment you are to measure a thermal property of nitrogen; its latent heat of vaporization.
Heat is a form of energy. The heat energy, Q, which must be added to a body to produce a one degree rise in the temperature of the body is called the heat capacity of the body. The heat capacity per unit mass of a material is called its specific heat, c. The heat energy added to the body is thus related to its rise in temperature, D T, by:
![]() (1)
(1)
if the specific heat is constant.
If a material undergoes a phase change, i.e., if it evaporates or melts or freezes, some heat energy may be absorbed or released without producing a change in temperature. The amount of heat absorbed (or released) per unit mass in the evaporation is called the latent heat of vaporization, L. We may think of this heat energy as the work required to overcome the molecular forces holding the material together as a liquid. The heat required to evaporate a mass, m, of the liquid is:
![]() (2)
(2)
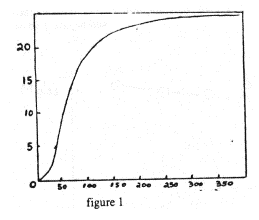
It is important to note that specific heats and latent heats are different for different materials. Moreover, for a single given material, specific heats are not constant but change with temperature. Near room temperature this variation can often be neglected, but at the low temperatures used in this experiment the temperature dependence of C is very important. A specific heat curve for a typical solid is shown in figure 1.
When two objects, one at a temperature Th and the second one at a lower temperature Tc are placed in contact, they come to equilibrium at a common final temperature, Tf. Energy conservation tells us that the heat energy lost by the hot object must equal the heat energy gained by the cold object in reaching Tf. This relation is the basis of calorimetry and is utilized in this experiment.
SPECIFIC OBJECTIVES:
When you have completed this experimental activity you should be able to: (1) define heat capacity, specific heat, and latent heat and give the units of measure of each; (2) sketch a curve showing the temperature variation of the specific heat of a typical solid; (3) describe the procedures involved in a calorimetry experiment; and (4) conduct an experiment to measure either the specific heat or the latent heat of a substance.
EXPERIMENTAL ACTIVITY:
Nitrogen has a boiling point of 77 K (-196oC). At this temperature it is a colorless liquid with a density of 0.8 g/cm3 and is in equilibrium with its vapor at atmospheric pressure. In this experiment you are to determine the latent heat of vaporization of nitrogen by observing the amount of nitrogen vaporized in cooling a sample of aluminum from room temperature (T1) to nitrogen temperature (TN). A double Styrofoam cup is filled about 3/4 full with liquid nitrogen; but, since its temperature is well below room temperature, heat is continuously boiled off. For accuracy in this experiment, it is necessary to distinguish between the boil-off due to this continuous "heat leak" and that caused by placing the aluminum into the nitrogen. If the cup with the nitrogen is placed on a scale and the mass of the system is recorded as a function of time, a curve similar to portion A-B of figure 2 results. Observations should be made at 20 second intervals for two minutes. During this time you should also measure room temperature -- the initial temperature of the aluminum block. With the clock still running, when you get to the two minute point, you should insert the aluminum block slowly into the liquid nitrogen. (CAUTION: liquid nitrogen can cause severe low temperature burns. The nitrogen will boil violently and splatter if the aluminum is lowered too quickly into the liquid.) Continue to make observations of the mass of the nitrogen at 20 second intervals for another six minutes. The mass will follow the curve indicated by portion B-C-D of figure 2 where it is understood that the mass of the aluminum is subtracted from the scale readings before plotting the data. The curve C-D should also be a straight line.

Begin your experimental work by conducting an experiment to determine the mass time curve of figure 2. The time interval between point A and point D will be about 8 minutes. Be sure to take enough points to determine the straight line C-D. Plot a graph from your data similar to figure 2. Determine the mass (D M) of nitrogen boiled off because of the aluminum block.
The heat gained by the nitrogen from the aluminum is:
![]() (3)
(3)
The heat lost by the aluminum is:
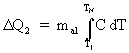 (4)
(4)
but since C changes significantly between room temperature and nitrogen temperature, the integral is not especially easy to calculate. Therefore, D Q2 must be found by a different method. The method of choice is simple calorimetry, like you did in Chemistry lab.
Remove the cup with liquid nitrogen and the aluminum block in it from the scale. Keep the block in the nitrogen. Weigh and record the mass of the inner cup and stirrer of the calorimeter. Fill the cup about 2/3 full of water, and weigh again to determine the mass of the water in the cup. Record the mass of the water, and its temperature (T2). Reassemble the calorimeter and check the water temperature again. Carefully transfer the aluminum block from the liquid nitrogen into the water in the calorimeter, and replace the cover. Stir the water until the temperature reaches equilibrium at T3. Record T3.
The heat gained by the aluminum as it warms up to T3 is equal to the heat lost by the water and calorimeter cup and stirrer in cooling to T3. Thus:
![]() (5)
(5)
Calculate D Q3. Show your work, being observant of units and significant figures. The value of ccal is 0.23 cal/g° C.
Placing the aluminum block in the calorimeter only brings the temperature up to T3. The heat needed to raise the temperature of the aluminum from T3 back to room temperature T1 is:
![]() (6)
(6)
where cal can be considered a constant over the small range between T3 and T1 and equals 0.23 cal/goC. Calculate D Q4.
The heat gained by the aluminum block in going from TN to T1 is equal to D Q3 + D Q4, and is the same as the heat lost by the aluminum when it was cooed by the nitrogen, so:
![]() (7)
(7)
Since the conservation of energy states that the heat lost by one object (the aluminum block as it cools) equals the heat gained by the second object (the liquid nitrogen which boiled off), it follows that D Q1 and D Q2 are equal, and thus:
![]() (8)
(8)
Thus you can calculate the latent heat of vaporization of nitrogen. Compare the value you obtained with the standard value found in the Handbook of Chemistry and Physics. Apply the percent error to your value of D M. Does an error in weighing of this magnitude seem likely? If not, what other source of error might exist?
FINAL SUMMARY:
Report your value for the latent heat of vaporization of nitrogen. How does your value compare to the standard value. Apply the percent error to your value of D M. Does an error in weighing of this magnitude seem likely? If not, what other source of error might exist? What additional conclusions can you make?