View the Equipment

When buying groceries, we are often interested in the price per pound. Knowing this, we can determine the price for a given amount of an item. Analogously, it is convenient to know the electric force per unit charge at points in space due to an electric charge configuration. Knowing this, we can easily calculate the force an arbitrary charge would experience at different points.

The electric force per unit charge is called the electric field intensity, or simply the electric field. By determining the electric force on a test charge at various points in the vicinity of a charge configuration, the electric field may be "mapped" or represented graphically by lines of force. The English scientist Michael Faraday (1791 - 1867) introduced the concept of lines of force as an aid in visualizing the magnitude and direction of an electric field.

In this experiment, the concept of the electric field will be investigated and the field lines for some charge configurations will be determined.

SPECIFIC OBJECTIVES:

When you have finished this experimental activity, you should be able to: (1) define the terms potential difference, equipotential surface, and electric field intensity; (2) understand the orthogonal relationship between equipotential surfaces and lines of force; (3) sketch the field lines around simple charge configurations; and (4) calculate electric field intensity from the spacing of equipotential surfaces.

The magnitude of the electrostatic force between two point charges q₁ and q₂ is given by Coulomb's law as

where r is the distance between the charges and the constant k = 9.0 x 10⁹ N m²/C². The direction of the force on a charge may be determined by the law of charges: Like charges repel and unlike charges attract.

The electric field is defined as the electrical force per unit charge, or E = F/q_o (N/C). Theoretically, the electric field is determined by using a positive test charge q_o. The test charge is taken to be positive by convention. In the case of the electric field associated with a single source charge q, the magnitude of the electric field a distance r away from the charge is

The direction of the electric field may be determined by the law of charges.

The electric field vectors for several series of radial points from a positive source charge are shown in Fig. 1(a). Notice that the lengths (magnitudes) of the vectors are smaller the greater the distance from the charge. Why? By drawing lines through the points in the direction of the field vectors, we form lines of force [Fig. 1(b)], which give a graphical representation of the electric field. The magnitudes of the electric field are not customarily listed, only the direction of the field lines. However, the closer together the lines of force, the stronger the field.

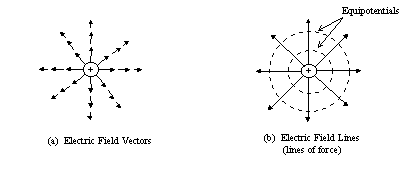
Figure 1

If a positive charge were released in the vicinity of a stationary positive source charge, it would move along a line of force in the direction indicated (away from the source charge). A negative charge would move along the line of force in the opposite direction. Once the electric field for a particular charge configuration is known, we tend to neglect the charge configuration itself, since the "effect" of the configuration is given by the field.

Since a free charge moves in an electric field by the action of the electric force, we say that work (W = Fd) is done by the field in moving charges from one point to another (e.g., A to B). To move a positive charge from B to A would require work supplied by an external force to move the charge against the electric field (force). The ratio of the work W done to the charge q_o in moving the charge between two points in an electric field is called the potential difference V_AB between the points:

(It can be shown that the potential at a particular point a distance r from a source charge q is
V = -kq/r.)

If a charge is moved along a path at right angles or perpendicular to the field lines, there is no work done (W = 0), since there is no force component along the path. Then along such a path [dashed-line paths in Fig. 1(b)], VAB = W/q_o = 0, and V_A must equal V_B. Hence, the potential is constant along paths perpendicular to the field lines. Such paths are called equipotentials (along an equipotential surface in three dimensions).

An electric field may be mapped experimentally by determining either the field lines (of force) or the equipotential lines. Static electric fields are difficult to measure, and field lines are more easily determined by measuring small electric currents (flow of charges) maintained in a conducting medium between charge configurations in the form of metal electrodes. The steady state electric field lines closely resemble the static field that a like configuration of static charges would produce. The current is measured in terms of the voltage (potential) difference by a high-impedance digital voltmeter. By locating a series of points all at the same voltage (potential), equipotential lines are easily determined. By mapping out several equipotential lines, and drawing the field lines perpendicular to the equipotentials, the field lines are easily displayed.

You will examine three different configurations in this experiment, an isolated point charge, a dipole, and a parallel plate capacitor. It will be necessary to paint the three patterns on separate sheets of conducting paper, as directed by the lab instructor, and let them dry for about twenty minutes. The "paint" is a liquid graphite preparation, and care should be taken to avoid getting the graphite on clothing or other items of value, as it is extremely difficult to remove. During the time the liquid graphite is drying, your instructor will show you the proper operation of the power supply, digital voltmeters, and field mapping apparatus.

Write your conclusions and attach the graphs to the lab report. Include in your summary the average value of Q from activity (A) and the electric field intensity calculated in activity (C). Comments on the symmetry of the various field patterns may help establish some conclusions about the fields.

Return to Table of Contents