Click here to see a video of the experiment

The flow of discovery in physic tends to be from observation to theory (formation of a plausible explanation in terms of more basic concepts) to experimentation (controlled observation). Hopefully, the experiments will confirm the theory or, if not, suggest the direction in which modification of the theory should proceed. In this experiment you are asked to examine whether or not momentum (a VECTOR defined by p=mv) is conserved in a two dimensional collision.

In the experiment, a sphere rolls down an incline made of a curved metal track and is projected horizontally from the edge of the table where it strikes a second sphere balanced on the end of a set screw. If the apparatus is carefully adjusted, the velocity vector of each ball immediately before and after the impact will lie in a horizontal plane. Neglecting air resistance, this horizontal velocity is independent of the vertical velocity acquired by the falling bodies and remains constant during the time of fall. This important concept is sometimes referred to as the principle of "independence of motions", and was discussed in class as part of the study of projectile motion.

Since the time of fall is likewise independent of the horizontal velocity, the horizontal distances traveled by the spheres while falling to the floor are measures of their velocities, and therefore their momenta and kinetic energies, immediately following the collision. That is to say, each of these kinematic properties is in some way directly proportional to the observed horizontal travel of the falling body.

SPECIFIC OBJECTIVES:

When you have completed this laboratory exercise, you should be able to: (1) state the principle of "independence of motions" and discuss its application to projectile problems; (2) state the conservation principles for linear momentum and for energy; and (3) describe the conditions under which momentum and kinetic energy are or are not conserved in two dimensional collisions.

The apparatus, while simple, is capable of reasonably accurate results when carefully used. Place the set screw directly in front of the channel of the track and about one radius distant from the edge of the track. Adjust the height of the set screw until a sphere rolling down the incline will make a center-to-center collision with a sphere at rest on the set screw. Once this height adjustment has been made, the height of the set screw should not be readjusted. In the work that follows the distance from the set screw to the ruler is always adjusted so that the incident sphere has just cleared the track when it collides with the rest sphere. For a "head-on" collision this means the set screw should be about 3 radii distant from the end of the track; for glancing collisions, a somewhat smaller distance is required.

Place a sheet of automatic carbon computer paper on the floor beneath the incline and mark the point, O, directly beneath the end of the track. Use the plumb bob to locate the point accurately. Tape the paper to the floor so that it can’t slide around. Move the set screw to the side so that it doesn’t interfere with the motion of the rolling sphere, and set the reference marker on the incline somewhere near the top of the incline. Allow one of the small steel spheres to roll down the incline, starting from the reference marker, and striking the floor at some point on the carbon paper. Repeat this some ten or fifteen times until a small cluster of points appears in the impact area. Label this area A.

Now set the apparatus for a glancing collision by adjusting the position of the set screw so that the incident sphere will roll down and cause a glancing collision with a sphere resting on the set screw. Best results will be obtained with the incident sphere being deflected about 30 or 40 degrees from the initial direction. Start the incident sphere from the reference marker, and repeat the identical glancing collision about 10 times. Mark the clusters of impact points as B and C. Make clear notations of which cluster of impacts belongs to the rolling sphere and which to the rest sphere.

Repeat the entire set of observations using a glass sphere for the rest sphere and a small steel sphere for the incident sphere. You will probably have to adjust the angle of the set screw a little to get consistent results. Again, mark the clusters of impact points and note which goes with which particle.

A third time, use the large steel sphere as the incident sphere, and a small steel sphere as the rest particle, and repeat the entire set of observations. Adjust the angle of the set screw as necessary to achieve proper deflection of the incident sphere, and carefully mark the clusters of points.

Finally, measure and record the masses of the spheres used in the experiment. Also, measure the distance of all of the spheres from the apparatus to the floor.

Begin by locating the center of the cluster of points labeled A. Then draw a line from the origin O to this center point, and label the line OA. Measure and record the length of this line.

Determine the time it takes an object to fall through the measured height. In experiment 5, this time was shown to be:

Record this time. Since the time of flight should depend only on the distance of vertical fall, all of the impacts should occur in equal times. Thus the horizontal velocities can be found from:

Determine the incident velocity by using equation (2) with the length of line OA and the time of fall from equation (1). Record this velocity as V.

Compute the average velocity of each sphere in the collision by measuring the distance from the origin, or point O, to the center of the cluster of impact points for that sphere, and using equation (2). Also, measure and record the angles between the line OA and the line to the center of impacts for each of the spheres in the collision.

Now construct an accurate scale drawing of the collision, using a scale of perhaps 1 cm represents 5 cm/s. Let the line OA represent the x-axis of your coordinate system, and find the linear momenta, and also x- and y-components, of the particles involved.

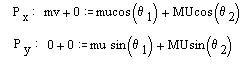
Compare the vector sum of the two momenta after collision with the momentum of the incident particle before collision. Is momentum conserved? To get a better grasp of how significant the error is, it is convenient to examine the x-components and y-components separately. Since the total linear momentum before the collision is in the x-direction, then it can be compared to the sum of the momenta in the x-direction after collision by use of percent difference. However, there is no y-component of momentum before collision, so analysis of the residual error in the y-direction requires the use of relative error. Find the quantitative measures of the errors for the x- and y- directions for this collision.

In general, a collision results in some kinetic energy being converted into heat energy. In a perfectly elastic collision, kinetic energy is conserved and no heat is produced. In such cases, and only those cases, we can write:

where the v and V are velocities before collision and the u and U are velocities after collision. Remember that energy is a scalar, and only the magnitude is a factor in such calculations. Determine whether kinetic energy was conserved in this collision by comparing the kinetic energy before collision with the kinetic energy after collision. What percent of the initial kinetic energy was "lost" in the collision? In light of the error determined for the momentum calculation, do you think that this change of kinetic energy is significant, or just within the probable error of the experiment? How does it affect your conclusions?

Analyze the second collision in the same manner as the first, by determining the velocities and angles of each of the particles, and then make a new scale drawing on a new page of paper. Compute the momenta of the particles, determine the components, compare the momenta before and after the collision, and find error percentages. Likewise, examine the kinetic energy before and after the collision, and determine whether or not it is conserved. Does it appear that the collision between glass and steel is more or less elastic, or about the same, as between two steel spheres?

Measure and analyze the third collision just as you have the first two, making a third scale drawing that shows this collision accurately. Analyze the momenta and kinetic energies as before, indicating the errors of your experiment as before. How does the larger mass of the incident sphere affect the experiment?

Report your percent error values for the momentum in each case. Answer all the questions that are asked in each section.

Return to Table of Contents