STANDING WAVES IN A STRING:
MELDE’S EXPERIMENT
Click here to see a video of the experiment
RATIONALE:
... took a musical string of brass, three quarters of a foot long and stretched it with a weight of six and five-eighth pounds, which I found matched by its vibrations a certain standard note in my organ. I found that a string of the same material and tension, fifteen feet, that is, twenty times as long, made ten recurrences in a second. I inferred that the number of vibrations of the shorter string must also be twenty times as great; and thus such a string must make in one second of time two hundred vibrations...
From the work of MERSENNE
By sound we mean that phenomenon which is capable of stimulating the sensation of hearing. Sound always originates in some type of motion. In many instances the source of sound is a standing wave in some vibrating body -- a drum head, the vocal cords of a guitar string or the air column in an organ pipe. Our goal in this experiment is to learn something about the formation of standing waves in strings and the boundary conditions which determine the pitch (frequency) of the sound produced.
Imagine a long string attached to the wall at one end. We grasp the other end, place the string under some tension, T, and vibrate this end up and down at some constant frequency, f.
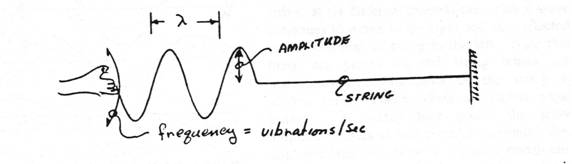
Successive crests and troughs are produced by the motion of the hand and are seen to move in succession down the string with constant speed, v. Such a wave is called a running wave. The distance between any two successive points in the wave train which have the same phase is called the wavelength, l. Careful study shows that the wavelength, frequency, and speed are related by the wave equation:
v = λ f (1)
Experiment also shows that the speed of the wave through the string is
independent of the frequency and amplitude of the wave and depends only upon
the characteristics of the media (the string) through which the wave moves.
This is a general property of many types of wave motion. Specifically the speed
of the running wave in the string is related to the tension in the string, T,
and the linear density of the string, m,
and (the mass per unit length of the string). The velocity is given by:
 (2)
(2)
When equations (1) and (2) are combined, we can solve for the frequency of
vibration. That is
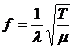 (3)
(3)
In this experiment we use an electrically driven vibrator to generate the wave and we are interested in the standing waves that are produced in the string under certain circumstances.
Consider the following situation. A running wave is produced by the vibration of the fork. The wave moves to the right where it encounters the wall. If the wall was not present and the string longer, the wave would have continued beyond the wall as shown by the dotted wave form. The wall is, however, present and the initial running wave (solid wave form) is reflected back into the string as a second running wave; see second sketch. This wave is moving toward the left.
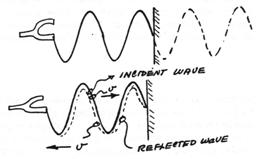
The details of the reflection process are rather involved and will be discussed more fully in class. Note, however, that the wave has "turned over" as a part of the reflection process. A nice simulation is here: StringWave
The instantaneous shape of the string is found by adding together the displacements that would be produced by the two waves acting independently. The series of sketches to the side show the resultant wave form (shape of the string) at six different times as the incident wave continues to move to the right and the reflected wave continues to move to the left. Note that there are points on the string where the instantaneous displacement of the string is always zero. These points are called nodal points. At intermediate points the wave amplitude builds up to a positive maximum, dies out, and then builds to a negative maximum. Thus, instead of seeing waves move successively down the string one sees the string vibrating in a series of loops -- each loop being just one half wavelength in extent. This type of wave is called a standing wave or a stationary wave.

Standing waves will form in the string only if certain "boundary conditions" are satisfied. Specifically, the length of the string must be some integral number of half-wavelengths for the initial running wave. Since the frequency of the wave is fixed by the vibrator, this means that we can adjust the tension in the string and therefore the wave speed (see equation (2)) until the wavelength (see equation (1)) satisfies this condition. Under these circumstances the string vibrates with the same frequency as the vibrator -- the system is said to be in resonance and the energy flows from the vibrator into the vibrating string. The amplitude of the string builds to quite large magnitudes at resonance.
SPECIFIC OBJECTIVES:
When you have completed this experimental activity you should be able to: (1) write and use the wave equation; (2) distinguish between running waves and standing waves; (3) describe the conditions that lead to standing waves in a string; (4) identify the factors that determine the speed of a running wave in a string; and (5) write and use the velocity equation for transverse waves in a string (equation (2)).
EXPERIMENTAL ACTIVITY:
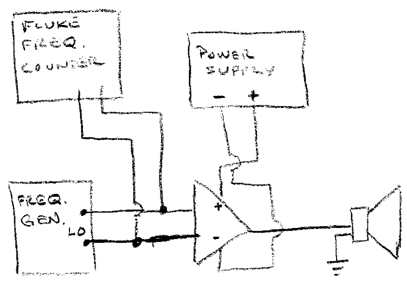
Connect the equipment as shown in the attached schematic. Attach the string to a rigid post on one end and pass the string over the pulley to a weight hanger on the other end. Place the vibrator about 6-8 inches from the fixed end. Place 150 grams total on the weight hanger, including the weight hanger. Before starting the vibrator, be sure to unlock it. Start the vibrator and adjust the frequency of the frequency generator until there is a node at the center of the string.
Adjust the frequency carefully so as to obtain the largest amplitude of the loops. Examine the wave motion carefully. Are all the loops of the same size (length)? Is the point where the string is attached to the vibrator a nodal point? How about the point where the string passes over the pulley? Does the speed referred to in equations (1) and (2) refer to any motion you can observe directly?
Record the number of vibrating segments of the string, n, the tension in the string (T in Newton’s), the wavelength (λ in m), and the frequency. Note that the best value for the wavelength is just twice the length of the loop of the vibrating string on the weight hanger end. Pay attention to the proper use of significant figures.
Repeat the above observations by varying the values of the mass from 150 grams to at least 750 grams in 100 gram increments. Finally, remove the string from the vibrator, untie all the knots, and measure carefully both the mass of the string and its length. Then calculate the linear density, m, by dividing the mass by the length. Record this value for reference.
ANALYSIS OF RESULTS:
Begin your analysis by plotting two graphs: (1) the wave velocity versus tension and (2) the square of the wave velocity versus tension. Draw these graphs properly, paying proper attention to coordinate labels, titles, etc. What conclusions do you draw from looking at these two graphs?
The v2 versus T graph should be a straight line. Determine the slope of that line, showing your work on the graph paper. The reciprocal of this slope should be the linear density of the string. Compute this value, and compare it with the number you obtained from direct measurement of mass and length. Use percent difference for your comparison.
Also use equation (3) to compute the theoretical frequency for each of the hanging mass values. Compare these values to the measured frequency readings recorded earlier. Compute the percent difference.
FINAL SUMMARY:
Report your average value for linear density. How did your two values compare? What is the relationship between the wave velocity and the tension? What additional conclusions can you make from this lab?
Be sure to answer the questions posed earlier in your summary.