 |
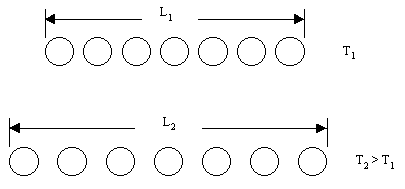
| Figure 1: Change in atomic spacing with increased temperature |
Thermal Expansion in One Dimension
Rationale:
It is fairly intuitive to understand that when things are heated they expand. This effect is used in many devices such as thermostats and mercury thermometers. Although the results of thermal expansion are helpful many times, there are several times that the results are destructive such as roads buckling and railroad tracks bending in the hot summer. A good understanding of thermal expansion will better equip you when dealing with this phenomenon.
Specific Objectives:
By the time you finish this lab you should be able to (1) read a dial gauge; (2) calculate the linear coefficient of thermal expansion for three types of metal; (3) graph change in length versus temperature; and (4) convert resistance values to temperature values.
Theory:
We will be investigating a group of materials that are labeled isotropic. Isotropic materials thermally expand in all directions equally. After investigating the thermal expansion phenomenon, it is evident that the average atomic spacing increases with temperature in most substances. Figure 1 below illustrates how the overall length of a string of atoms, representing the atoms in our experimental tubes, will increase with temperature.
 |
| Figure 1: Change in atomic spacing with increased temperature |
Keep in mind, the average atomic position is just an average. In reality the atoms oscillate around their average position. Given a few material parameters, we can predict how much the length, height, and width of an object will increase with temperature. Experimental observations suggest that the greater the temperature increase, the larger the increase in length. Also, the larger the original length of the object the greater the increase in length as it is warmed up. Mathematically we can state this using equation 1 below, where α is a proportionality constant and is material dependent.
|
|
|
Equation 1 |
Experimental Activity:
Measuring the rod length: Length (L) is determined by measuring from the inner edge of the stainless steel pin on one end, to the inner edge of the angle bracket at the other end. Record in a table the length of the copper, aluminum, and steel tubes, respectively.
Place the rod in the expansion base by placing the stainless steel pin into the slotted mounting block. The other end of the rod has an angle bracket mounted on its side. Now slide the dial gauge into the mounting block next to the angle bracket on the tube. Press the spring-loaded dial gauge against the angle bracket until it registers zero, then secure it with a small screw. Next, attach the thermistor lug to the middle of the tube using a threaded thunbscrew. Make sure the thermistor lug is aligned with the axis of the rod for maximum contact between lug and rod. (The lug has a saddle bend in it to ensure that the lug is properly aligned). Place the foam insulator over the thermistor lug for more accurate readings. Now connect your ohmmeter to the banana jacks labeled THERMISTOR in the expansion base. Record the room-temperature resistance value displayed on your ohmmeter in a table. Next connect the steam generator via a flexible hose to the end of the tube farthest from the dial gauge. Elevate this end of the expansion base by using the small wooden block. The elevation is needed to allow condensation to drain from the tube. Make sure that you place a Styrofoam cup at the other end to catch the draining water. Finally, turn on the steam generator and begin warming up the tube. Once the tube starts to expand it will take approximately 2 minutes to reach its maximum length. After the tube appears to stop expanding, wait an additional 2 minutes for equilibrium to be established and accurately record both resistance and dial gauge readings. Each increment on the dial gauge is equal to 0.01 mm. Make sure you record these values in a table for the respective tubes. Repeat this procedure for each tube.
Analysis of Data:
Convert each resistance reading to a temperature value using equation 2 below. T is calculated in degrees Celsius, and R must be in Ohms (Ω). This equation is accurate to within one percent. Make sure these values are recorded properly in a table.
|
|
|
Equation 2: Conversion of resistance to temperature. |
On one graph place two points for each material. The horizontal axis represents the temperature and the vertical axis represents the tube length. Plot one point for room temperature and one for the final temperature. Connect the two points with a straight line and determine the slope. Equation 1 tells us the slope equals αL. From this slope value, calculate the linear expansion coefficient for each material.
Final Results:
Clearly indicate your values for linear expansion coefficient for each tube by using the slope of the graph. Report the percent difference between your calculated linear expansion coefficient value and the textbook value for each tube.
Questions: