Superconductivity Lab
View magnet lift up and how to get the magnet to spin
MOTIVATION:
Superconductivity was discovered by H. Kamerlingh-Onnes in Holland in 1911 as a result of his ability to make liquid helium. In Onnes' time superconductors were simple metals like mercury, lead, bismuth, etc. The elements became superconductors only at the very low temperatures of liquid helium. During the 75 years that followed, great strides were made in the understanding of how superconductors worked. Over that time, various alloys were found that were superconductors at somewhat higher temperatures. Unfortunately, none of these alloy superconductors worked at temperatures much more than 23 Kelvin. Thus, liquid helium remained the only convenient refrigerant that could be employed with these superconductors.
Then in 1986, researchers at an IBM laboratory in Switzerland discovered that ceramics from a class of materials called perovskites were superconductors at a temperature of about 35 Kelvin. This event sparked great excitement in the world of physics, and earned the Swiss scientists a Nobel prize in 1987. As a result of this breakthrough, scientists began to examine the various perovskite materials very carefully. In February of 1987, a perovskite ceramic material was found that was a superconductor at 90 Kelvin. This was very significant because now it became possible to use liquid nitrogen as the refrigerant.
There are several advantages in using liquid nitrogen instead of liquid helium. Firstly, the 77 Kelvin temperature of liquid nitrogen is far easier to attain and maintain than the chilly 4.2 Kelvin of liquid helium. Liquid nitrogen also has a much greater capacity to keep things cold than does liquid helium. Most importantly, nitrogen constitutes 78% of the air we breathe, and thus unlike liquid helium, for which there are limited sources, it is literally dirt cheap.
SPECIFIC OBJECTIVES:
Having completed this laboratory exercise, a student will: a) understand the fundamental concepts of superconductivity; b) understand and have observed the Meissner effect; c) have learned the composition of high temperature superconductors; d) have measured the critical temperature of 1-2-3 type superconductors using two different methods.
THEORY:
The theoretical understanding of superconductivity is extremely deep, and far beyond the scope of this course. However, some of the fundamental terms, concepts, and phenomena are relatively easy to follow, and will be discussed here.
Superconductors have the ability to carry an electrical current without loss of energy. Unlike normal conductors of electricity in which the current is carried by individual electrons, in superconductors the current is carried by pairs of electrons called Cooper pairs. When the electrons move through a solid in Cooper pairs they are impervious to the energy absorbing interactions that normal electrons suffer. To form Cooper pairs, a superconductor must operate below a certain temperature called the critical temperature or Tc. Superconductors made from different materials have different values of Tc. For the new ceramic superconductors in this experiment, Tc is about 90 Kelvin.
It is not yet clear that these ceramic superconductors indeed do conduct by means of Cooper pairs as described by the 'BCS' theory. In fact, a new theory called the 'Resonant Valence Bond' theory appears to be more effective in describing the superconductivity phenomenon in these new materials. This theory may explain the gradual onset of superconductivity at a temperature around Tc in the ceramic materials, as compared with the very sudden transition to the superconductivity state in metallic superconductors.
Since there is no loss in electrical energy when superconductors carry an electrical current, relatively narrow wires made of superconductivity material can be used to carry huge currents. However, there is a certain maximum current (actually current density) that these materials can be made to carry, above which they stop being superconductors. This maximum current is referred to as the critical current or Ic. Much effort is being expended in order to increase the value of critical current for the new ceramic superconductors.
It has long been known that an electrical current in a wire creates a magnetic field around the wire. The strength of the magnetic field increases as the current in the wire is increased. On account of their ability to carry large electrical currents without loss of energy, superconductors are especially suited for making powerful electromagnets. Furthermore, if the electrical current travels only through a superconductor without having to pass through a normal conductor, then it will persist forever resulting in the formation of a powerful permanent electromagnet. These permanent currents in a superconductor are referred to as persistent currents.
The magnetic field generated by the superconductor in turn, however, affects the ability of the superconductor to carry electrical currents. In fact, as the magnetic field increases, the values of both Tc and Ic decrease. When the magnetic field is greater than a certain amount, the superconductor can carry no current, and also Tc decreases to 0 Kelvin. This maximum magnetic field is called the critical field, or Hc. Again, this is a large field and even the powerful rare earth alloy magnets we will use in our experiments will not significantly affect the superconductors.
Composition of High Temperature Superconductors
The new ceramic superconductors are a class of minerals collectively called perovskites. Perovskites are metal oxides that have a formula that normally has 3 oxygen atoms for every 2 metal atoms. In any one perovskite, there can be a mixture of several different metals. For example, in the superconductors in this experiment, the metals are yttrium (Y), barium (Ba), and copper (Cu). Using the standard valence values for the metallic elements, one would expect the chemical formula YBa2Cu3O9. Surprisingly, scientists have found that these superconductors are about 2 oxygen atoms short, and instead have the approximate formula YBa2Cu3O7.
One should note that the proportions of the 3 different metals in the ceramic perovskite superconductors are in the ratio of 1 to 2 to 3 for yttrium to barium to copper respectively. Thus, this particular type of superconductor is often referred to as a 1-2-3 superconductor. This fact also indicates the proportions in which the original constituents need to be mixed to make these superconductors.
Three separate chemical compounds containing yttrium, barium, and copper respectively are mixed in proportions such that the three metals are in the ratio of 1-2-3. The resulting mixture is then heated and cooled several times in a kiln or electrical furnace, usually in the presence of oxygen. The amount of oxygen in the 1-2-3 compound can vary depending on the way it was made. If the sample is short on oxygen, it will be green, and will not be a superconductor. If on the other hand it has the right amount of oxygen, it will be black. This black material is a superconductor.
Scientists are discovering that many other metals may be substituted for the ones in our sample. In early 1988, scientists in Japan found a compound of Bismuth, Strontium, Calcium and copper that is perhaps an even better superconductor than the 1-2-3 compound. While the resulting materials are also superconductors, they may have widely differing values of Tc, Hc, and Ic.
The perovskites are ceramics, and thus share many properties with other ceramics. One of these properties is brittleness. This has particularly bedeviled technologists because it makes it very difficult to make the flexible wires that are needed for practical applications.
Meissner Effect:

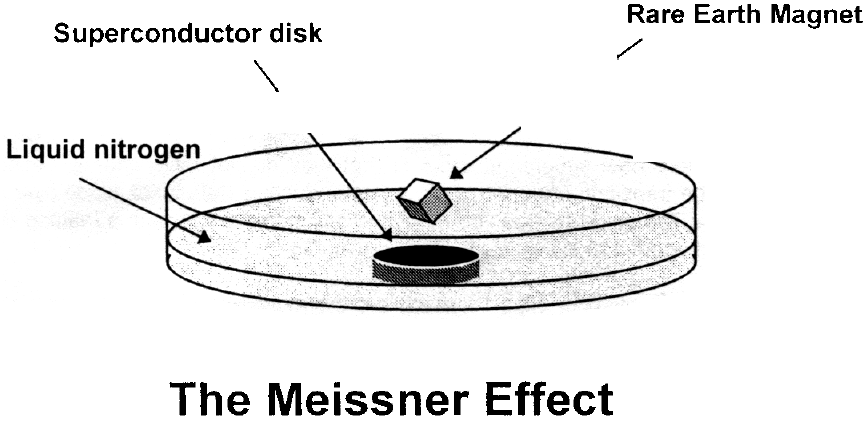
One of the properties of superconductors most easy to demonstrate, and also very spectacular, is the Meissner Effect, after the person who first discovered it in 1933. This is a magnetic repulsion effect that occurs because superconductors are strongly diamagnetic. As your textbook indicates, diamagnetic materials are those that when placed in the presence of a strong magnetic field, will react by aligning internally to produce a field opposed to the external field. This produces a repulsion that in most materials is too weak to notice.
It is important to realize that Faraday's Law of Induction does not explain magnetic repulsion in a superconductor. Very simply, when a material is in a superconductivity state, the superconductor will not allow any magnetic field to enter it. This is because microscopic magnetic dipoles are induced in the superconductor that oppose the applied field. This induced field then repels the source of the applied field, and will consequently repel the magnet associated with that field. This implies that if a magnet were to be placed on a superconductor when the superconductor was above its critical temperature, and then it was cooled below Tc, the superconductor would then exclude the magnet field of the magnet and try to levitate the magnet above the superconductor. This is clearly the Meissner Effect, and not Faraday's Law.
For the experiment to be successful, the strength of the magnet must be large in relation to its weight. One would not expect to levitate a weak but heavy iron magnet above a superconductor, and so we use the very powerful, but very small, rare earth magnets for this demonstration. One other note of interest is that the Meissner Effect seems to be a bulk phenomenon of the 1-2-3 superconductor. If two or more superconductivity disks are stacked, the magnet is levitated higher than if only one disk is used.
SAFETY CONSIDERATIONS:
Liquid Nitrogen:
Liquid Nitrogen is a cryogenic material with a boiling temperature of 77K (-196oC). As a result of this very low temperature, improper handling can result in physical harm to persons in the lab. Please observe the following safety rules.
Superconductor materials:
The ceramic superconductors deserve some special handling to prolong their useful life and avoid shortening yours. In particular, one needs to remember that these samples are made of the oxides of various metals, and need to be treated like toxic materials. Please observe the following rules for handling the superconductor pellets.
EXPERIMENTAL ACTIVITY:
Part A: Meissner Effect
Carefully pour a small amount of liquid nitrogen into the Styrofoam container until the liquid is about 1/4 inch deep. Using the tweezers, carefully place the black superconductor disk flat in the liquid. Ideally, the liquid will be just flush with the top of the disk.
Using the tweezers, pick up the provided magnet and place it on the top of the superconductor disk. Instead of settling down on the surface of the superconductor, the magnet will float a few millimeters above the superconductor. This is a demonstration of the Meissner Effect.
If you set the magnet rotating with the tweezers, you will note that it continues to rotate for a long time. This is a crude demonstration of a frictionless magnetic bearing using the Meissner effect. You may have to look carefully to see the rotation, but watch for it and think about how it could be used. Also, try to push the magnet away from the center of the superconductor and see what happens. How could this be useful?
Part B: Measuring Critical Temperature
There is a second superconductor at your workstation that is encased in metal and has a pair of leads attached to it. The leads are connected to a thermocouple placed at the lower superconductor surface, and designed to measure accurately the temperature of the superconductor. The thermocouple is a device made by joining two different metals at a point called a junction. The temperature of the junction causes a voltage to be produced that is related to the temperature of the junction, which is then read by a sensitive voltmeter attached to the leads of the thermocouple. A conversion chart is found on page 11 of the Superconductor manual.
To increase the accuracy of the experiment, a fixed gain amplifier is available which multiplies the voltage by a factor of 100. When using this in combination with your voltmeter, make sure to divide the reading by 100 before you convert it to a temperature using the chart.
Carefully straighten the thermocouple leads and attach the clip leads of the digital voltmeter to them. Note the reading of the thermocouple at room temperature, and then immerse the superconductor in liquid nitrogen and check the temperature again. The readings should be about -0.16 millivolt at room temperature and 6.43 millivolt in liquid nitrogen (77K). Any great variance indicates a problem that needs to be corrected before you go any further.
Remove the device from the liquid nitrogen and place it flat so that the superconductor surface is exposed. Balance the rare-earth magnet so that it floats via the Meissner effect over the center of the disk. Record the voltmeter readings every 10 seconds, noting the reading at which the magnet comes to full rest on the surface of the disk. This temperature is the critical temperature, Tc.
mV to Kelvin Conversion
One of the mysteries of the 1-2-3 superconductors is that they do not have sharply defined critical temperatures. Typically, the transition from normal to superconductivity state takes place over a range of about 5 Kelvin. Check with others in your lab to see what critical temperature they found. How consistent are your temperature and theirs?
Part C: Resistance as a Function of Temperature
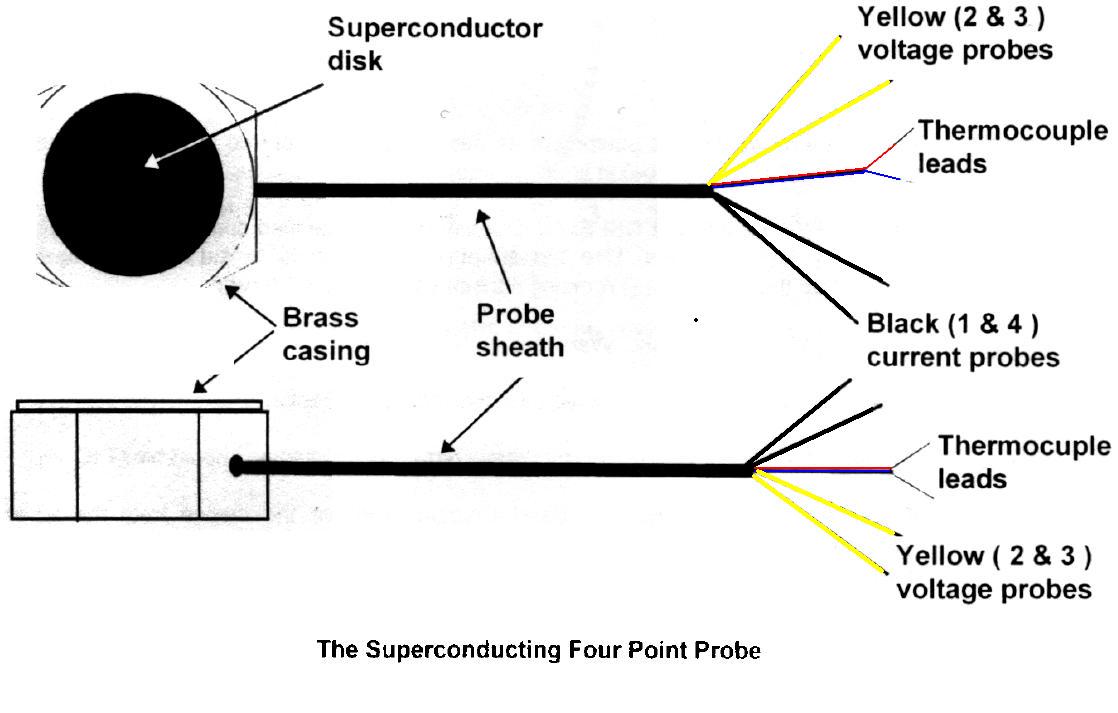
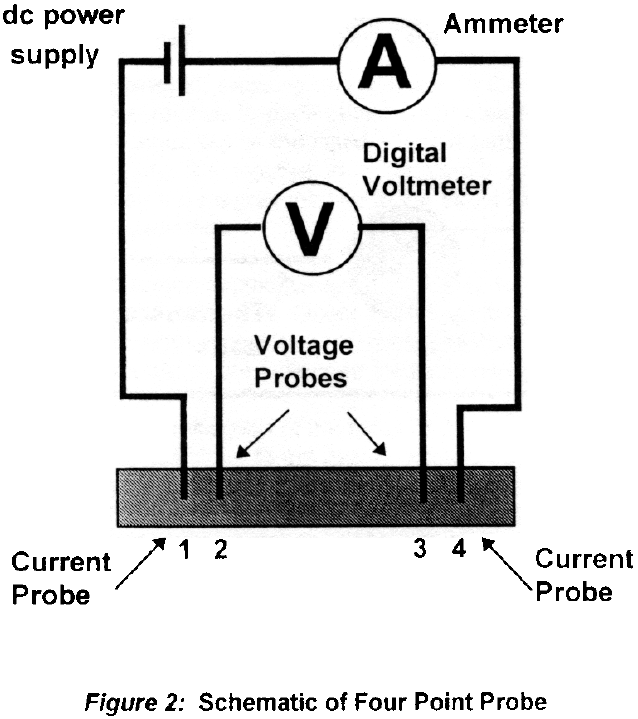
Set up the measurement equipment as described above, but do not as yet immerse the device (four point probe) in liquid nitrogen. Use the fixed gain amplifier for both V23 and the thermocouple voltage.
Insert the device into the Sand Cryostat and carefully fill it with liquid nitrogen. Use the sheathed wire bundle to suspend the device.
Ensure that the current (I14) remains constant at less than 0.5 Amp (the exact value is arbitrary). The nitrogen boils furiously Wait until the boiling subsides
Record the voltage V23, and the voltage across the thermocouple junction. It is important that the temperature start below the critical temperature of the superconductor, so make sure the corresponding thermocouple voltage is high enough before you allow it to start warming. V23 should start near zero. The thermocouple temperature reading should be near 77 K.
Watch the rate of temperature change of the superconductor, and use the liquid nitrogen to insure that the rate of increase is plenty slow. As the device warms, continuously monitor the value of V23. Record the thermocouple voltage each time V23 is recorded.
When the thermocouple voltage readings correspond to a temperature above 120 K, you should have plenty of useful data. At this point you may disassemble the circuit, and take the thermocouple device out of the Sand Cryostat. Make sure you immediately begin to dry the superconducting device to avoid any water damage to it.
ANALYSIS:
Use Excel to make a connected scatter-plot of Resistance vs. Temperature. Note that neither of these were measured directly, rather calculated from measurements of voltage and/or amperage. This graph should reveal the critical temperature of the superconductor YBa2Cu3O7. Compare the value you found in Part B using the Meissner effect with the one you found from your plot in part C using a percent difference calculation.
QUESTIONS: