MATHEMATICAL NOTES FOR PHYSICS LAB
SIGNIFICANT FIGURES:
The digits required to express a number to the same accuracy as the measurement it represents are known as significant figures. If the length of an object is measured as 10.34 cm, this quantity is said to be measured to four significant figures. If written as 0.0001034 km, it is still measured to only four significant figures since the zeros preceding the 1 only indicate the position of the decimal point. The zero between the 1 and the 3 is a significant number.
If the above measurement of 10.34 cm is made with a meter stick, the last digit recorded is an estimated figure representing a fractional part of a millimeter division, the smallest division shown on the meter stick. All recorded data should include the last estimated figure in the result, even though it may be zero. If this measurement had appeared to be exactly 10 cm, it should have been recorded as 10.00 cm, since with the meter stick you can estimate to 0.01 cm.
The reading of 10.34 cm means that the value actually lies between 10.33 cm and 10.35 cm, or that there is an uncertainty of 0.01 cm in the measurement. This is an error of 0.01 cm in the measured length of 10.34 cm, or a fractional error of .01/10.34, which is less than .001 or 0.1% approximately.
Probably the most difficult thing for most students is keeping the correct number of significant figures. It is important to realize that your calculator will not do it for you. You must do it in spite of your calculator’s display. For instance, if you measure the radius of a circle to be 6.75 cm, the circumference of the circle will be computed as:
![]()
Your calculator will display 42.411501, but since your measurement was accurate to only 3 significant figures, your proper answer should also have 3 significant figures, or 42.4 cm. To know how many significant figures should be kept in the result of a computation, the following rules should be observed:
SUMS AND DIFFERENCES
Quantities to be added or subtracted should be measured to the same number of decimal places regardless of the number of significant figures. The result of either operation should retain no more decimal places than can be trusted in the quantity having the fewest trustworthy decimal places.
Example: To add three lengths, 10.07 cm, 0.0126 cm, and 4.1 cm, imagine them written in column form as:
10.07 which 10.1
0.0126 reduces 0.0
4.1 to 4.1
The result is reported as 14.2 cm and not as 14.1826 cm.
NOTE: the reduction in significant figures and the rounding off takes place before the mathematical operation of adding is performed.
PRODUCTS AND QUOTIENTS
Quantities which are to be multiplied or divided should be measured to the same number of significant figures. The common practice is to carry only one doubtful or "non-significant" figure in all calculations until the final result, when the doubtful figure is dropped. A product or a quotient should have only as many significant figures as the factor having the fewest number of significant figures.
Example: The following laboratory problem, in which all figures are significant --
![]()
should be rewritten with three significant figures (2 actual significant and 1 doubtful figure) as --
![]()
and then solved with the result being expressed as 7900 cm/sec and not as 7932.22 cm/sec.
EXACT NUMBERS
In many equations, there are certain exact numbers, which should be noted. For example, in the equation for circumference given earlier, the factor 2 is an exact number, which has not one significant figure, but an infinite number of significant figures. Exact numbers arise from theory and are not part of a measurement. They should be distinguished from measured quantities, and not considered when trying to determine the correct number of significant figures for a result.
ROUNDING NUMBERS
In dropping figures which are not significant, the number which remains is a rounded number, not a truncated number. This means that if, for instance, the number 44.357 is reported to 3 significant figures, it would become 44.4, because the number is closer to 44.4 than it is to 44.3.
ANALYSIS OF ERROR
Several statistical measures are used to express the accuracy or estimated accuracy of an experimental result in a quantitative form. Those with which we shall be concerned are: (a) percent errors; (b) percent difference; (c) relative error; (d) standard deviation; and instrument error.
PERCENT ERROR is defined as 100 times the ratio of the error made in measuring a quantity to the correct or best accepted value of the measured quantity.
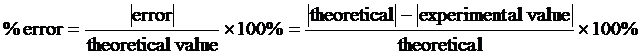
The value of the error is the arithmetic difference of your measured or computed value minus the correct value which may give a plus or minus value. This measure is useful only when there is a universally accepted value with which to compare your results.
PERCENT DIFFERENCE is used when there is not a universally accepted value to compare with, but there are two independently measured values which are considered to be equally valid. In this situation, percent difference is defined to be the difference of the two values divided by the average of the values, times 100 to make it a percent. In equation form, it is:
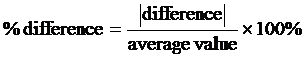
RELATIVE ERROR is used when the expected answer is zero. This measure of error compares the amount of error with the size of the quantities that entered into the computation, and thus relates the magnitude of the error with the magnitude of the measurement. If, for instance, two quantities A and B were added, and the expected result was zero, the experimental result might not be exactly zero. The relative error is then the error divided by the sum of the absolute values of A and B, times 100 to make it a percent. In equation form, it is:
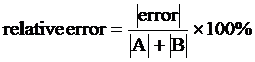
STANDARD DEVIATION is a commonly used measure of experimental accuracy when there is no universally accepted value to compare with, and no independently found second value to compare with. Realizing that no outside value exists for comparison, the value is compared against itself, by making a large number of determinations of the value and checking for consistency. This check will determine the extent of random errors, but will not reflect the effect of systematic errors, such as calibration errors in the instruments.
In this situation, a number of observations of the experimental quantity, say N of them, are made. The experimental result is the mean, or average, of these N observations. Random errors in the individual observations tend to cancel each other in the mean; however, this cancellation is ordinarily not complete for a finite number of observations. The standard deviation of the mean gives us an estimate of the completeness of this cancellation effect, i.e., of how closely we should expect the mean to approximate the real value of the quantity which we are measuring. Statistically, the formula is given as:
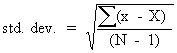
Here X is the mean of the N observations, x is an individual observation, and the summation denotes that we should sum up the (x - X)
2 for all N observations.The significance of the standard deviation is that it permits an estimate of the probability that the real value of the quantity being studied lies within some interval around the mean value found experimentally. Basically, the following is valid:
(a) It is twice as likely that the real value is within one standard deviation of the mean than it is to be further away; or, for a larger number of observations, 68.3% of them will fall within one standard deviation of the mean.
(b) It is twenty times as likely for the real value to be within two standard deviations of the mean than it is to be further away; or, for a large number of observations, 95.45% of them will fall within two standard deviations of the mean.
(c) It is nearly 400 times as likely for the real value to be within three standard deviations of the mean than it is to be further away; or, for a large number of observations, 99.73% of them will fall within three standard deviations of the mean.
It is common practice to use 3 standard deviations to estimate the accuracy of an experiment. We can then define the estimated percent error as:
![]()
Although the standard deviation may at first appear complicated, the calculations and ideas involved are worth mastering, for the use of this measure of uncertainty is not unique to physics. It is widely used in medical, behavioral, and social sciences as well as in educational research. It is important to have some knowledge of the measures of the uncertainty to which all measurements are subject, especially in this day of contending claims of environmental problems and the proper utilization and control of natural resources. Only in this way can we hope to judge which claims rest on a foundation of empirical evidence and which are only unsupported speculations.
INSTRUMENT ERROR is used to determine how much error should be expected due to the limitations of the measuring devices. Each device has a limitation on the precision of its measurement. In equation form, it is:
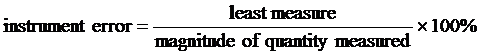
Least measure refers to the smallest division marked on the instrument. Typically, instrument error will be much smaller than the total error present in an experiment.