CIRCULAR
MOTION AND CENTRIPETAL FORCE
Click here to see a video of the first part of the
experiment
Click here to see a video of the second part of the
experiment
Click here for an excel template
RATIONALE:
Newton realized that an object which experienced a zero net force would move with uniform motion in a straight line. Therefore the moon, which orbited the earth, must experience a non-zero force. Analysis of the acceleration of an object in circular motion indicates that the force which acts on the object in circular motion must be directed at the center of the circular motion, and such a force is called a centripetal force. For the moon, the question to be answered was what force could supply the necessary centripetal force to keep the moon in its nearly circular orbit. Newton deduced that it must be the gravitational force. The gravitational pull of the earth on the moon supplied just the required centripetal force to keep the moon in its orbit.
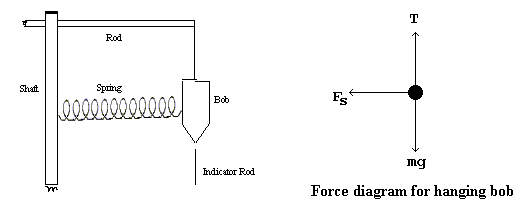
In the laboratory other systems can be devised to examine centripetal force. For this experiment, an apparatus consisting of a pendulum bob suspended from a rod of adjustable length is rotated about a vertical axis. A rotating shaft supports the rod and turns on ball bearings. A light spring is connected between the shaft and bob and supplies the centripetal force. A portion of the shaft is knurled to allow easy rotation of the shaft by hand. An adjustable indicator point allows the experimenter to see when the bob is in the vertical position. With this apparatus the centripetal force supplied by the spring can be compared with the required force as calculated from theory.
SPECIFIC OBJECTIVES:
When this laboratory exercise is completed the student will be able to: (1) convert angular speed from rev/sec to rad/sec; (2) determine the net force acting on a rotating object; (3) measure the force required to stretch a spring a specified amount; (4) calculate the centripetal force required for a rotating object; and (5) determine the major source of experimental error for this experiment.
THEORY:
When the apparatus is at rest the spring holds the bob near the rotating shaft. As the rotation rate of the apparatus is gradually increased the bob moves outward slowly until it hangs vertically. At this point the forces on the bob are as shown in figure 1. The tension forces in the supporting cord just equal the weight of the bob and the centripetal force is supplied totally by the spring. Notice that the bob is NOT in equilibrium, as there is nothing which equalizes the centripetal force.
At this point the bob of mass m moves at constant speed v in a
horizontal circle of radius r. The centripetal acceleration of the bob
is v2/r,
directed to the center of the circle. The net force is then:
![]() (1)
(1)
Now the velocity must be measured in terms of the radius r and the
number of revolutions per second N so that:
![]() (2)
(2)
The force then becomes:
![]() (3)
(3)
and the required centripetal force for the object can be calculated from equation (3). The force of the spring itself can be measured directly by pulling the spring out to the same position, using hanging weights. Then we have two independent measurements of the force which can be compared with each other.
Measure the mass of the hanging bob. Record the mass to the nearest tenth of a gram.
Set the hanging bob about 15 to 17 cm from the axis of the shaft. Measure the distance carefully and record it. Set the indicator point so that it is directly under the bob when the bob is just hanging vertically. To do this, it is easiest to temporarily disconnect the spring from the bob, so that the bob will hang vertically. Adjust the indicator point carefully, as you will use it to determine when the bob is rotating with the correct speed.
Attach the spring to the bob and rotate the shaft until the speed is just sufficient to make the bob hang vertically as it rotates. Measure the time required to rotate through at least 20 revolutions, and record the value in a data table. Be careful as you count the revolutions, as this tends to be a source of error. Repeat the measurement until you have three consistent values which vary by less than 0.2 seconds. Be sure to keep the speed as consistent as possible during the measurement, and line things up carefully so that the bob is really in the vertical position during the entire measurement. Record all of your time values, and compute the average number of revolutions per second.
Now attach the string and weight hanger to the bob, pass the string over the little pulley, and place sufficient weight on the weight hanger to pull the bob exactly out to the vertical position. Record the weight (including the weight hanger) and convert the value to Newtons by multiplying the hanging mass (in kg) by 9.81 m/s2 (gravitational acceleration).
Now increase the radius of the hanging bob to about 20 to 22 cm, and repeat the measurements at the longer radius. Be sure to do both the timed observations and also the spring force determination.
Finally, add a 50 gram mass to the hanging bob and secure it in place with the little knurled nut on the top of the hanging bob. Leave the radius at the distance used in the previous part. Repeat both force measurements with the "heavier" hanging bob.
Analyze your data by computing the centripetal force using equation (3). Compare this value with the force required to pull the bob out to the same position. Find the percent difference of these values. Analyze all three cases in the same manner.
FINAL SUMMARY:
Report the average force values for each case. What do you notice about the centripetal force as the radius changes? What effect does a change in mass have on the system? Explain why these changes occur. Draw careful conclusions from your observations.
QUESTIONS:
- Calculate the instrument
error for the measurements of time, mass, and radius. Do this for each of
the three cases of your experiment. Also include total instrument error
for each case. (Total instrument error is as follows: Mass Error + Radius
Error + 2 *
Time Error.)
- How does the total
instrument error compare to the percent difference?
- What does your answer
to question #2 indicate about the experimental results?
- Which of the three
measuring devices is the most significant source of error?
Explain why this is the case.
- In what way(s) would
you modify the experiment to reduce the error?