 (1)
(1)NEWTON’S SECOND LAW OF MOTION:
THE ATWOOD MACHINE
Click here to see a video of the experiment
RATIONALE:
The second law of motion is one of the most powerful laws in physics. In principle it allows an observer to calculate the forces acting on a body from measurements of the body’s motion. Conversely, if one knows the forces acting on an object, the future motion of that body can be predicted. This experiment utilizes an "Atwood machine" to illustrate and, in a sense, verify the second law.
Suppose you were called upon to measure the acceleration due to gravity, g, using an ordinary stopwatch and a falling body. You might drop the body, time its fall over a distance, h, and apply the equations of uniformly accelerated motion. In this case, the formula:
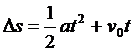 (1)
(1)becomes:
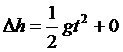 (2)
(2)From the measured values of h and t, the acceleration g can be determined. If, however, you attempt this experiment, some difficulties are encountered. For small values of h, it is difficult to measure t accurately. For larger values of h, the speed of the object may increase to the point where air resistance introduces a non-negligible but unknown force. The simple Atwood machine offers a way around these difficulties.
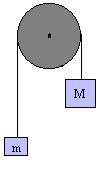
The machine consists of two equal masses M suspended from a light thread which passes over a massless and frictionless pulley. If we now add a small additional mass, m, to one side the system will be unbalanced and will accelerate with an acceleration, a. This acceleration is much less than that of a freely falling body and can be readily measured with an ordinary meter stick and stopwatch. As we will see, one can then infer the value of g from this measured acceleration, a. In effect, the Atwood machine "expands" the time scale being measured. Physicists frequently develop instruments or devices that serve to "magnify" observed quantities in a similar way.
SPECIFIC OBJECTIVES:
When you have completed this experimental activity you should be able to: (1) apply the equations of motion to a simple system with constant linear acceleration; (2) write and use the equation relating the weight and mass of an object; (3) write Newton’s second law for the linear case (F=ma), define the quantities referred to in the second law, and give the units of each; (4) sketch an Atwood machine and explain its purpose; and (5) derive an expression relating the acceleration of an Atwood machine to the acceleration of a freely falling body.
EXPERIMENTAL ACTIVITY:
Using the material furnished, construct an Atwood machine. Adjust the height of the pulley in such a way that one mass can fall at least 100 cm to the floor without striking the second mass and without the second mass striking the pulley. Use a mass of about 100 grams plus a weight hanger on each side of the Atwood machine.
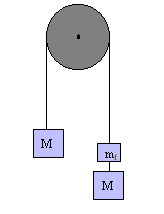
The pulley you have been furnished is probably far from frictionless. Evaluate this possibility by setting the masses in motion (at low speed) and observing to see if they continue to move with constant speed. If friction is present in the system, it can be compensated for by very patiently adding small masses to one side of the machine until it will just move at constant speed after being set into motion.
Once friction has been adequately compensated we add an additional mass, m, called the acceleration rider to the system. When released, the machine is now unbalanced and will accelerate with uniformly accelerated motion. Record the values of M, and mf.
Using an acceleration rider of about 10 grams, allow the system to move from rest through some measured distance (perhaps 50 cm) to the floor. Measure the distances and times of each of the points carefully. In a data table, record the distance of fall and the corresponding times.
Repeat the ENTIRE SET of measurements for one more acceleration rider -- perhaps 20 grams. You should then have measurements for each of the 2 acceleration riders that you used.
ANALYSIS OF RESULTS:
Consider the masses on the left-hand side of the Atwood machine. These masses descend with constant acceleration, a, and the equations of uniformly accelerated motion apply. Among these is equation (1), which takes the form of equation (2) for the conditions of our experiment.
Equation (2) can be rewritten as:
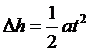 (3)
(3)Construct a graph of distance versus time using the first set of data obtained, and obtain a quadratic regression equation. The second derivative of this equation should be the acceleration, a. Determine the magnitude of the acceleration by multiplying the "a" coefficient by 2. Make an additional graph in the same way for the other set of data.
Calculation of g
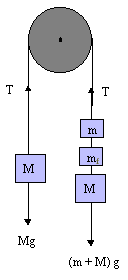
The Atwood machine has been sketched again, this time with the forces that act on the suspended masses displayed. Notice that both upward forces are represented by the same tension T, even though the masses on the two sides are not equal. Why is this permissible? Why are the downward forces represented as mg and not just m? Be sure you understand these two items fully.
We now write two equations, one for each side of the Atwood machine:
![]() (right side of machine)
(right side of machine)
and
Note that we have omitted an (mf)g term from the forces side of the second equation because this force is balanced by an opposing frictional force. We have, however, included this mass on the right-hand side of the equation since this mass does have to be accelerated along with the rest of the system.
If we now subtract these two equations we get:
which becomes:
which we can then solve for g to get:
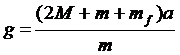 (6)
(6)Once you are sure that equation (6) is correct, you may use it to determine the value of g for each of the two sets of data. Show your calculations and the results clearly. Find the average of the two values and compare it with the accepted value of 9.81 m/s2.
FINAL SUMMARY:
Report your average value of g. Which acceleration rider gave you the largest percent error? Which one gave you the smallest percent error? What conclusions can you draw from these? Do you feel the friction rider adequately compensates for friction? What conclusions can you draw about Newton’s second law from this experiment?
QUESTIONS: